Data sets
For the purpose of this book some built-in data sets are used. Most of the built in data sets are available via rapaio.datasets.Datasets class. This is an utility class which provides some standard data sets used in many statistical and machine learning text books. There are a few which we will use for the purpose of this tutorial.
Iris data set
The Iris flower data set or Fisher's Iris data set is a multivariate data set introduced by Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis. It is sometimes called Anderson's Iris data set because Edgar Anderson collected the data to quantify the morphological variation of Iris flowers of three related species.
Two of the three species were collected in the Gaspé Peninsula all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus.
The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). There are for measures for each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.
Frame iris = Datasets.loadIrisDataset();
iris.printSummary();
This is the summary of this data set:
Frame Summary
=============
* rowCount: 150
* complete: 150/150
* varCount: 5
* varNames:
0. sepal-length : num | 2. petal-length : num | 4. class : nom |
1. sepal-width : num | 3. petal-width : num |
sepal-length sepal-width petal-length petal-width class
Min. : 4.300 Min. : 2.000 Min. : 1.000 Min. : 0.100 setosa : 50
1st Qu. : 5.100 1st Qu. : 2.800 1st Qu. : 1.600 1st Qu. : 0.300 versicolor : 50
Median : 5.800 Median : 3.000 Median : 4.350 Median : 1.300 virginica : 50
Mean : 5.843 Mean : 3.057 Mean : 3.758 Mean : 1.199
2nd Qu. : 6.400 2nd Qu. : 3.300 2nd Qu. : 5.100 2nd Qu. : 1.800
Max. : 7.900 Max. : 4.400 Max. : 6.900 Max. : 2.500
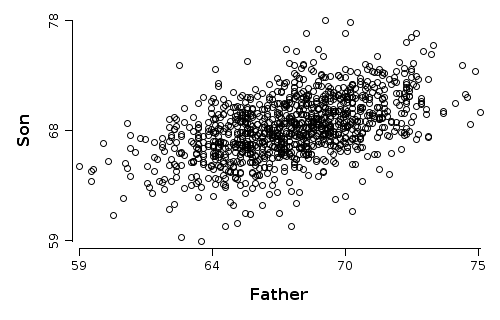
Pearson's Height Data
This simple data set comes from a famous experiment by Karl Pearson around 1903. The number of cases is 1078. The original data values were rounded to produce heights to the nearest inch.
Frame fs = Datasets.loadPearsonHeightDataset();
fs.printSummary();
The summary of the data set shows the two numeric variables with heights for fathers and sons.
Frame Summary
=============
* rowCount: 1078
* complete: 1078/1078
* varCount: 2
* varNames:
0. Father : num | 1. Son : num |
Father Son
Min. : 59.000 Min. : 58.500
1st Qu. : 65.800 1st Qu. : 66.900
Median : 67.800 Median : 68.600
Mean : 67.687 Mean : 68.684
2nd Qu. : 69.600 2nd Qu. : 70.500
Max. : 75.400 Max. : 78.400